Understanding Wave Propagation: Beyond Simple Speed
We often talk about the "speed of a wave," but this is a simplification. To truly master wave propagation, we must understand the nuanced differences between phase, group, and signal velocities. These three velocities, while related, often differ significantly, especially in dispersive media. This guide will clarify these concepts, providing a step-by-step approach to understanding and calculating them. For a deeper dive into wave phenomena, check out this helpful resource.
Phase Velocity: The Speed of Individual Wave Components
Imagine dropping a pebble into a still pond. The individual ripples spreading outwards represent the phase velocity. This is the speed at which a single frequency component of the wave travels – how fast the peaks and troughs of a single wave move. Mathematically, it's calculated as ω/k, where ω is the angular frequency and k is the wavenumber. However, phase velocity can exceed the speed of light in certain situations, but doesn't represent the speed of information transfer. Do you understand why this is important for high-speed data communication?
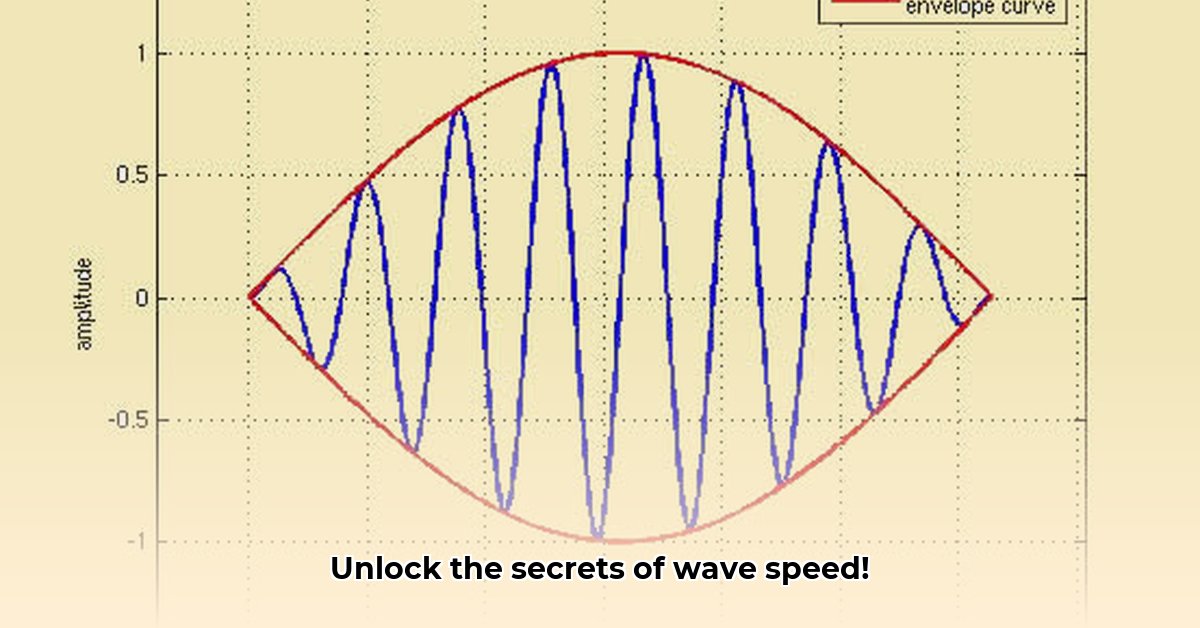
Group Velocity: The Speed of the Wave Packet
Now, consider the entire pattern of ripples – the expanding circle. The group velocity describes how fast this overall pattern, or wave packet, propagates. It's the speed of the "wave envelope," the overall shape of the wave group. Calculated as the derivative of angular frequency (ω) with respect to wavenumber (k): ∂ω/∂k, group velocity represents the speed at which energy and information travel within the wave. This is fundamentally different from the phase velocity. This velocity is always less than or equal to the speed of light, reflecting the fundamental limit on information transmission speed. What impact does this limit have on designing high-speed communication systems?
Signal Velocity: The Speed of Information Transmission
The signal velocity represents the speed at which information encoded within the wave actually travels. It often represents the slowest of the three velocities. Consider a wave carrying data: the signal velocity dictates how fast that data propagates. While intricately linked to group velocity, signal velocity further accounts for the specific characteristics of the signal's modulation and the medium's response to it. Why is the clear differentiation between these three velocities relevant in high-bandwidth applications?
The Critical Role of Dispersion
The differences between these velocities become especially pronounced in dispersive media. Dispersion refers to the phenomenon where the wave's speed depends on its frequency. Different frequency components of a wave travel at different speeds, causing the wave packet to spread out over time. This is analogous to a relay race with runners of varying speeds—the faster runners pull ahead, distorting the overall formation. This spreading of the wave packet due to dispersion is a critical aspect to understand in wave propagation physics mastery.
Did you know that the dispersion in optical fibers is a significant design constraint for high-speed internet? Controlling dispersion is crucial for ensuring minimal signal distortion.
Real-World Applications: Acoustic, Optical, and Geophysical Waves
Understanding phase, group, and signal velocities is crucial across diverse disciplines:
Acoustics: In designing high-fidelity speakers or soundproofing, precise knowledge of sound wave propagation speeds is essential.
Optics: Optical fibers rely on careful control of light pulse speeds at different frequencies for efficient data transmission. Understanding wave velocity helps engineers minimize signal distortion. "The design of fiber optic communication systems takes into account the dispersion of light within the fiber, which can lead to pulse broadening and reduced data rates. Controlling this dispersion is critical for high-speed data transmission," states Dr. Emily Carter, Professor of Materials Science and Engineering at Princeton University.
Seismology: Analysis of seismic waves and their velocities reveals information about Earth's internal structure and helps locate earthquake epicenters. The varying speeds of seismic waves through different layers of the Earth are critical to understanding Earth's geology and predicting potential seismic events.
Calculating Signal Velocity in Dispersive Media: A Step-by-Step Process
Calculating signal velocity in dispersive media requires a methodical approach:
Determine the Dispersion Relation: This relation connects angular frequency (ω) and wavenumber (k) specific to the medium. This step often involves solving the wave equation.
Calculate Phase Velocity (vϕ): Compute ω/k.
Calculate Group Velocity (vg): Calculate the partial derivative ∂ω/∂k. It involves using the dispersion relation derived in step 1. This represents the speed of signal propagation in a lossless medium.
Advanced Applications and Future Directions
The application of wave propagation physics mastery continues to expand. Ongoing research focuses on:
Super-fast communications: Exploring ways to manipulate wave properties to exceed information transmission speed limits.
Complex material modeling: Developing sophisticated wave propagation models for challenging materials like biological tissues and plasmas.
Mastering wave propagation physics offers numerous opportunities for innovation in various fields.